Linear regression – Web Education in Chemistry

The best line through a set of points

Lambert-Beer's law states that there is a linear relationship between the concentration of a compound and the absorbance at a certain wavelength. This property is exploited in the use of calibration curves, which enable us to estimate the concentration in an unknown sample.
A straight line is defined by the equation

$y=ax+b$

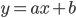
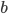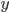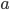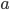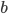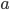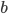Here, $b$ denotes the intercept of the line with the $y$ -axis and $a$ denotes the slope. The usual method to calculate the best line is called "Least Squares (LS)" regression. This method finds values for $a$ and $b$ in such a way that the sum of the squared differences of the datapoints with the fitted line is minimal. This is done by setting partial derivatives for $a$ and $b$ to zero.
Two examples of data sets are given below. The first is a calibration line for the determination of Cd with Atomic Absorption Spectroscopy (AAS); the second a comparison of two analytical methods, a reference method and a new one. Select one of the examples and click the "Submit" button. It is also possible to fill in your own data for 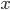$x$ and $y$ .

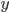LS regression: assumptions

1. Errors (in this case: deviations from the ideal straight line) are only present in the 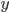$y$ -variable (i.e. the absorption) and not in 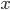$x$ (concentration). Does it make a difference which variable we put on the 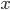$x$ -axis and which on the 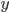$y$ -axis? To check this, select one of the two prefab datasets or enter your own data, and press the "Submit" button.

2. The errors in y are independent and normally distributed with a constant variance over the whole range of the calibration line. Several violations of this assumption can be seen in practice (make a choice and be sure that you check all three options!):

Continue with the questions on this subject.